When Bayesian Uncertainty Becomes Memory - A Path to Continual Learning

“Knowing what you don’t know” is a phrase that’s often misunderstood in Bayesian deep learning. The naive interpretation is that a model simply becomes uncertain when it encounters data different from its training set. In reality, a Bayesian model’s “knowledge” is initially governed by its prior — an abstract construct that’s usually far from human-interpretable. So while the model may know what it doesn’t know, we humans often don’t know what it knows.

Towards the end of my PhD, I was working with my friend and co-author Francesco D’Angelo on a paper exploring this very issue (D’Angelo* & Henning*, 2021). In this blog post, I discuss how the notion of “knowing what you don’t know” becomes meaningful for continual learning once uncertainty is directly tied to the observed training data. In our paper, we illustrate examples where epistemic uncertainty begins to mirror the underlying data distribution.

This connection gives uncertainty a generative flavor. And when uncertainty becomes generative, something profound happens — continual learning is solvable as a side product. If uncertainty reflects the density of what has been learned, then sampling from regions of low uncertainty is equivalent to replaying what the model already knows. That’s the essence of what we called uncertainty-based replay.

A Short Detour: Bayesian Learning and Continual Learning

For a proper introduction to Bayesian statistics and continual learning, see Chapters 3 and 4 of my thesis: (Henning, 2022).

Continual learning is usually described as the challenge of learning a sequence of tasks — say, recognizing trees, then flowers, then animals — without forgetting what came before. Most machine-learning models struggle because learning a new task often overwrites parameters acquired from previous tasks, causing catastrophic forgetting.

In principle, Bayesian statistics already offers a mathematically elegant solution. The recursive Bayesian update tells us exactly how to incorporate new data:

\[p(\mathbf{w} \mid D_{1:t}) \propto p(D_t \mid \mathbf{w}) p(\mathbf{w} \mid D_{1:t-1})\]

This formula says: use your previous posterior as the new prior — the old knowledge naturally carries forward.

If we could compute this update exactly, continual learning would be solved. The model would integrate new information while preserving everything it had already learned. But in practice, these updates are intractable for complex models, and approximations like variational inference or Monte Carlo sampling often fail to capture true posteriors.

In this post, we explore a different perspective: instead of trying to solve the Bayesian update, we use Bayesian uncertainty itself as a tool for continual learning.

It’s a method that only works if the prior is chosen just right — but when that’s the case, uncertainty itself becomes memory.

When Uncertainty Becomes Generative

What a Bayesian model “doesn’t know” depends entirely on the prior (the assumptions it carries before seeing any data). A good prior encodes an inductive bias: it guides generalization, shapes how the model extrapolates from few examples, and defines what kind of uncertainty is meaningful.

In Bayesian neural networks, however, priors are typically defined in weight space, often as zero-mean Gaussian distributions. This is mathematically convenient but conceptually arbitrary. Its effect in function space, where the model actually operates, is unpredictable and usually meaningless.

As a result, the model’s uncertainty tells us little about the structure of the data it has seen — it’s just variance around arbitrary parameter settings.

But there’s another way to think about priors. Suppose we choose a prior that reflects the data distribution — one that, once updated with real examples, concentrates uncertainty along the data manifold. Then the posterior uncertainty ceases to be an abstract measure of ignorance. It becomes a map of experience.

In this view, uncertainty isn’t merely epistemic; it’s generative. Sampling from it can recreate plausible variations of what the model has already seen.

Adapted from Fig. 3 in (D’Angelo* & Henning*, 2021). These plots show the epistemic uncertainty in a 2D input space for a Gaussian process with two different priors — an RBF kernel (left) and a periodic kernel (right). In the RBF case, regions of low uncertainty closely follow the data distribution, showing how the prior shapes uncertainty in function space.

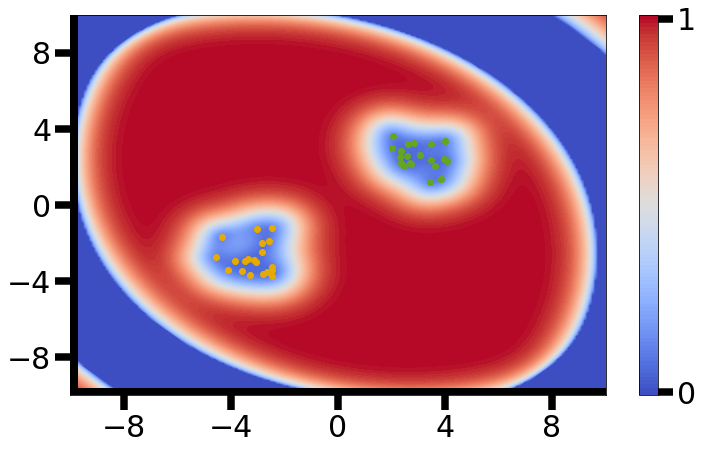
Francesco recognized a beautiful connection here: in a Gaussian process with an RBF kernel, epistemic uncertainty is mathematically related to the inverse of a kernel density estimate with a Gaussian kernel (cf. Section C in the supplementary material).

In other words, the regions where the model feels most certain are precisely those where data density is highest — and that’s the bridge between uncertainty and memory.

Uncertainty-Based Replay

Once uncertainty becomes generative, continual learning stops being a separate problem.

A model that can sample its own past from uncertainty no longer needs external memory. Its uncertainty is the memory — a compact, probabilistic summary of past experience encoded in the posterior.

Whenever a new task arrives, we can sample synthetic examples from regions of low epistemic uncertainty — regions corresponding to what the model already “knows”. By mixing these synthetic samples with new observations, we effectively reconstruct an IID-like dataset approximating all observed experience (past + present). Training on this joint dataset prevents forgetting, just as if we had stored all past data explicitly.

This is the core idea behind uncertainty-based replay. In classical generative replay, continual learning requires two models: one for the task, another (often a VAE or GAN) to imitate past data.

Here, the Bayesian model simultaneously serves as learner and generator, exploiting its own uncertainty structure to replay experience.

Adapted from Fig. S9 in (D’Angelo* & Henning*, 2021). The left plot shows a Bayesian model trained on all regression data at once, split into two tasks (separated by the dashed line). The middle plot shows a Bayesian model trained only on task 1 (black dots), together with pseudo-inputs sampled from low-uncertainty regions (yellow dots). These generated samples are combined with the task 2 data (right plot). Despite being trained continually, the final model closely matches the joint training solution on the left.

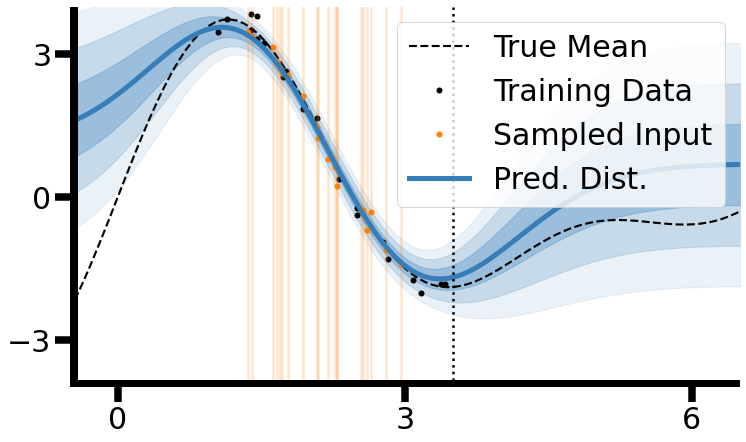
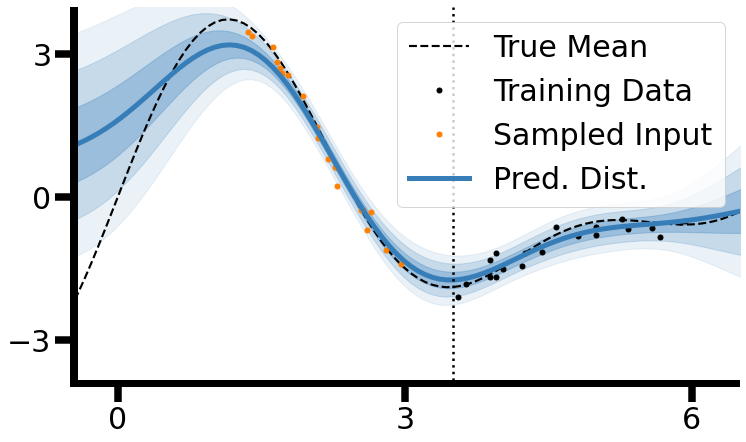
In practice, this idea only works if epistemic uncertainty correlates with data density — as in the RBF-kernel case above. When that alignment holds, the posterior variance effectively is a generative model of past observations. When it doesn’t, uncertainty degenerates into noise and replay collapses.

Still, the conceptual simplicity is striking: by inverting uncertainty into density, a model can recreate its own past and learn continuously — no extra parameters, no external memory, just a well-chosen prior.

Closing Thoughts

This is a conceptual demonstration — a small excursion into how Bayesian models could, in principle, learn continually.

In theory, it’s beautifully simple: uncertainty doubles as memory. In practice, it’s brutally difficult. Choosing a prior that induces the right inductive bias — and approximating a posterior rich enough to preserve it — remains an open challenge.

Yet the idea is compelling. If the brain operates (at least approximately) as a Bayesian system, then uncertainty-based replay might not be far from what biology already does.

Sleep could act as nature’s generative replay phase, resampling from internal uncertainties to consolidate and refine past experiences.

Continual learning, then, is not just about retaining the past — it’s about imagining the past in ways that preserve learning and enable future adaptation.

The question whether inputs are valid for the problem a neural network is trying to solve has sparked interest in out-of-distribution (OOD) detection. It is widely assumed that Bayesian neural networks (BNNs) are well suited for this task, as the endowed epistemic uncertainty should lead to disagreement in predictions on outliers. In this paper, we question this assumption and show that proper Bayesian inference with function space priors induced by neural networks does not necessarily lead to good OOD detection. To circumvent the use of approximate inference, we start by studying the infinite-width case, where Bayesian inference can be exact due to the correspondence with Gaussian processes. Strikingly, the kernels derived from common architectural choices lead to function space priors which induce predictive uncertainties that do not reflect the underlying input data distribution and are therefore unsuited for OOD detection. Importantly, we find the OOD behavior in this limiting case to be consistent with the corresponding finite-width case. To overcome this limitation, useful function space properties can also be encoded in the prior in weight space, however, this can currently only be applied to a specified subset of the domain and thus does not inherently extend to OOD data. Finally, we argue that a trade-off between generalization and OOD capabilities might render the application of BNNs for OOD detection undesirable in practice. Overall, our study discloses fundamental problems when naively using BNNs for OOD detection and opens interesting avenues for future research.

Natural intelligence has the ability to continuously learn from its environment, an environment that is constantly changing and thus induces uncertainties that need to be coped with to ensure survival. By contrast, artificial intelligence (AI) commonly learns from data only once during a particular training phase, and rarely explicitly represents or utilizes uncertainties. In this thesis, we contribute towards improving AI in these regards by designing and understanding neural network-based models that learn continually and that explicitly represent several sources of uncertainty, with the ultimate goal of obtaining models that are useful, reliable and practical. We start by setting this research into a broader context and providing an introduction to the fields of uncertainty estimation and continual learning. This detailed review can constitute an entry point for those interested in familiarizing themselves with these topics. After laying this foundation, we dive into the specific question of how to learn a set of tasks continually and present our approach for solving this problem based on a system of neural networks. More specifically, we train a meta-network to generate task-specific parameters for an inference model and show that, in this setting, forgetting can be prevented using a simple regularization at the meta-level. Due to the existence of task-specific solutions, the problem arises of having to infer the task to which an unseen input belongs. We investigate two major ways for solving this \emphtask-inference problem: (i) replay-based and (ii) uncertainty-based. While replay-based task-inference exhibits remarkable performance on simple benchmarks, our implementation of this method relies on generative modelling, which becomes disproportionately difficult with increased task complexity. Uncertainty-based task-inference, on the other hand, does not rely on external models and scales more easily to complex scenarios. Because calibrating the uncertainties required for task-inference is difficult, in practice, one often resorts to models that should \emphknow what they don’t know. This can in theory be achieved through a Bayesian treatment of model parameters. However, due to the difficulty in interpreting the prior knowledge given to a neural network-based model, it also becomes difficult to interpret what it is that the model \emphknows not to know. This realization has implications beyond continual learning, and more generally affects how current machine learning models handle unseen inputs. We discuss the intricacies associated with choosing prior knowledge in neural networks and show that common choices often lead to uncertainties that do not intrinsically reflect certain desiderata such as detecting unseen inputs that the model should not generalize to. Overall, this thesis compactly summarizes and contributes to the advancement of two important topics in nowadays deep learning research, uncertainty estimation and continual learning, while disclosing existing challenges, evaluating novel approaches and identifying promising avenues for future research.

When Bayesian Uncertainty Becomes Memory - A Path to Continual Learning

A Short Detour: Bayesian Learning and Continual Learning

When Uncertainty Becomes Generative

Uncertainty-Based Replay

Closing Thoughts

References

Enjoy Reading This Article?